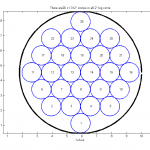
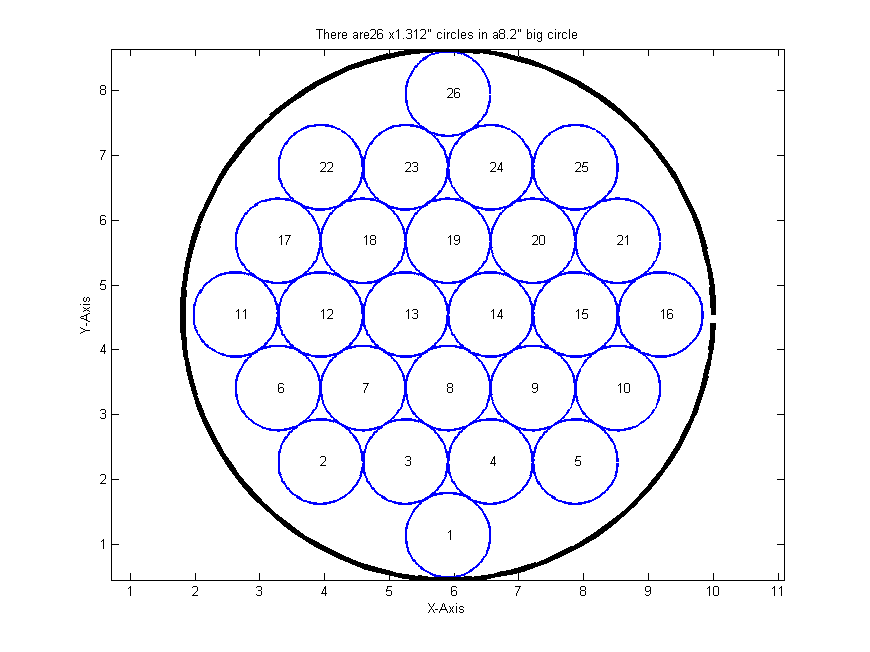
Packing Circles in a Big Circle
The problem statement is,’ How many circles can you pack in one big circle?’. It may sound like a trivial problem, but when you sit down to solve it, you quickly realize that it isn’t. I learned from experience the night I did this sub-project.
Why did I bother doing this? Well, I needed to figure out an approximate number of ‘circles’ that could fit in a ‘big circle’ so I can go ahead with main design project. In this case, ‘small circles’ can be electrical cables and the ‘big circle’ can be a conduit, raceway, or a sheath.

In electrical installations, the quantity of electrical cables pulled through a conduit is determined by the relevant NEC (National Electric Code) section. (image from www.ecmweb.com)
Without a solution like the one described herein, I resorted to good old SolidWorks to quickly pattern small circles, fit one large circle and then count the little ones. This approach works when you want to estimate a small number of ‘circles’, as the population increases, SolidWorks may start to run into graphics issues because of too many sketches.
I did find a few academic algorithms/formulas in literature, but I didn’t have the luxury of reading long mathy papers. However, there were some industrial solutions that I found. For example, for packing cables in cylindrical conduit in the solar/electrical industry, the National Electric Code has pre-calculated results that only work for a given combinations of wire sizes and fill-factors. I didn’t have a fill factor in mind nor did I want one: I needed to see visually what the result looks like.
In conclusion, to the best of my searches at the time, there wasn’t a tool/easy solution to do this so I decided to make my own. My solution is pretty easy to follow as I commented step-by-step in the following code.
The code
%AUTHOR: JONAH KADOKO % 1/26/13 % THIS PROGRAM SOLVES FOR THE NUMBER OF CIRCULAR OBJECTS ONE CAN FIT IN A % BIG CIRCLE % SCOPE: % 1. THIS PROGRAM HAS NOT BEEN OPTIMIZED TO FIND MAXIMUM NUMBER OF % SMALL CIRCLES. % 2. THIS PROGRAM IS RECOMMENDED FOR USE BY PEOPLE TO ESTIMATE THE NUMBER % OF CIRCULAR OBJECTS IN PRACTICAL APPLICATIONS. clear all;close all; % User Variables: d=1.312; % diameter of the small circles D=8.2; % diameter of the big circle % there is some round off error, play around with D or d to get a sweet % spot % Internal Variables: r=d*0.5; % radius of small circles R=D*0.5; % radius of the big circle rot_R=2*r; % radius from the center of the big circle deltaY=sqrt((2*r)^2-r^2); % the vertical distance between adjacent % small circles ang=0:0.05:2*pi; % for plotting circles xC=r*cos(ang);yC=r*sin(ang); XC=R*cos(ang);YC=R*sin(ang); % MAIN ALGORITHM % 1. Solve for the number of circles that can be arranged % straight in a row. % Also equal to the longest row of circles in a hexagon nRowMax=floor(R/r); if mod(nRowMax,2) % odd nRowMax=nRowMax+2; bigCirclePos(1,2)=0.5*(nRowMax-1)*deltaY; bigCirclePos(1,1)=(nRowMax-1)*r; else % even nRowMax=nRowMax+2; bigCirclePos(1,2)=0.5*nRowMax*deltaY; bigCirclePos(1,1)=(nRowMax+1)*r; end % 2. Draw circles in a big square % 3. Weed-out small circles that do NOT CircleTempPos=zeros(nRowMax^2,2); nSquare=0;nCircle=0;nonCircle=0; for row=1:nRowMax for col=1:nRowMax nSquare=nSquare+1; % for all even rows, an offset of r is applied CircleTempPos(nSquare,1)=(col-1)*2*r+(1+(-1)^(row))*0.5*r; CircleTempPos(nSquare,2)=(row-1)*deltaY; rot_R=sqrt((CircleTempPos(nSquare,1)-bigCirclePos(1,1))^2+... (CircleTempPos(nSquare,2)-bigCirclePos(1,2))^2)+r; if rot_R<=R nCircle=nCircle+1; inscribedCircle(nCircle,:)=CircleTempPos(nSquare,:); else nonCircle=nonCircle+1; nonInscribedCircle(nonCircle,:)=CircleTempPos(nSquare,:); end end end figure(1) % 4. Plot circles, that fit and those that do not % solve xy position of circles % a) small circles that fit for n=1:nCircle plot(inscribedCircle(n,1)+xC,inscribedCircle(n,2)+yC,'b',... 'LineWidth',2); hold on % plot(inscribedCircle(n,1),inscribedCircle(n,2),'ob'); text(inscribedCircle(n,1),inscribedCircle(n,2),num2str(n)); end % b) big circle plot(bigCirclePos(1,1)+XC,bigCirclePos(1,2)+YC,'k','LineWidth',4); % plot(bigCirclePos(1,1),bigCirclePos(1,2),'ok'); % c) circles that do not fit % plot(nonInscribedCircle(:,1),nonInscribedCircle(:,2),'or',... % 'MarkerSize',5,'MarkerFaceColor','r') title(strcat('There are ',num2str(nCircle),' x ',num2str(d),... '" circles in a ',num2str(D),'" big circle')) xlabel('X-Axis') ylabel('Y-Axis') hold off axis equal