Thermal analysis of box-type solar cookers (2/2)
 The MATLAB implementation of the thermal model below:
The MATLAB implementation of the thermal model below:
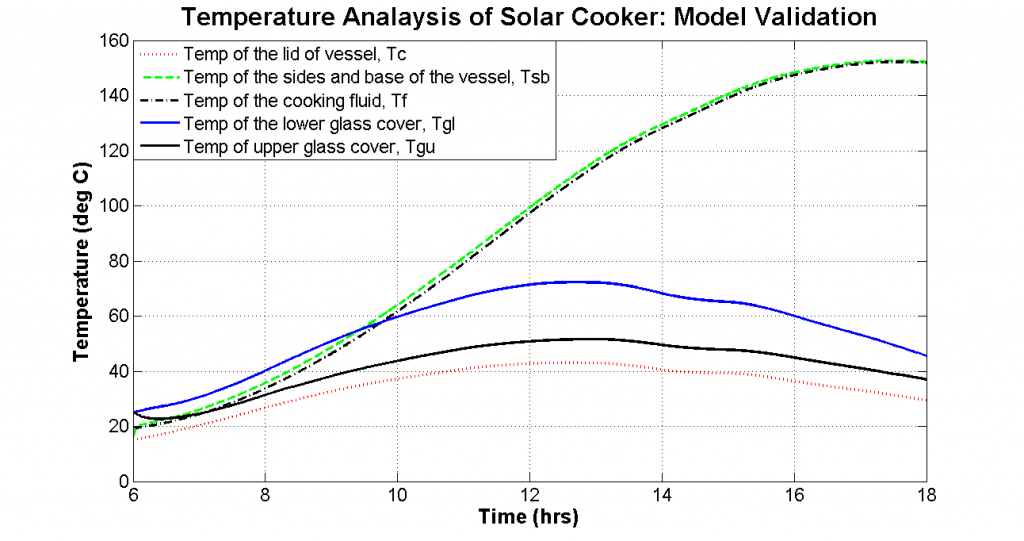
The temperature plot of solar cooker to validate the mathematical model. In a practical situation, once the cooking fluid reaches 100 ̊ C, cooking fluid temperature remains constant because of latent heat of vaporization.
MATLAB script
% Author: Jonah Kadoko % Project: Solar Fundamentals, Fall 2014 % Instructor: % Description: This is the main script for modelling a solar box-type % cooker. In this mathematical model, several coatings of commercially % avialable coatings will be i nvestigated. % T : is a 5x1 array of temperatures in the following order: % T(1): Temperature of the lid of vessel, Tc % T(2): Temp of the sides and base of the vessel, Tsb % T(3): Temp of the cooking fluid, Tf % T(4): Temp of the lower glass cover, Tgl % T(5): Temp of upper glass cover, Tgu addpath('C:\Users\<User>\Documents\MATLAB'); % T(1) - % Input Variables clc t_S=6*3600; % [s] starting time t_F=12*3600; % [s] time to stop the iterations, 4.770 seems to be max time % t_Span=linspace(0,t_F,floor(t_F/t_Step)); % Calculations options=odeset('Stats','off'); % set the end conditions [t, T]=ode45(@temp_Profile,[0 t_F],[75 80 80 25 25],options,t_S);
Plot Results
clf; % clear all figures axes('FontSize',14); T_max=max(max(T)); axis([t_S/3600 (t_F+t_S)/3600 0 T_max]) plot((t+t_S)/3600,T(:,1),':r','LineWidth',2); hold on; plot((t+t_S)/3600,T(:,2),'--g','LineWidth',2); plot((t+t_S)/3600,T(:,3),'-.k','LineWidth',2); plot((t+t_S)/3600,T(:,4),'-','LineWidth',2); plot((t+t_S)/3600,T(:,5),'-k','LineWidth',2); grid on; title('Temperature Analaysis of Solar Cooker: Model Validation','FontWeight','bold','FontSize',20) xlabel('Time (hrs)','FontWeight','bold','FontSize',16) ylabel('Temperature (deg C)','FontWeight','bold','FontSize',16) legend('Temp of the lid of vessel, Tc','Temp of the sides and base of the vessel, Tsb',... 'Temp of the cooking fluid, Tf','Temp of the lower glass cover, Tgl',... 'Temp of upper glass cover, Tgu'); hold off;
Calculate the glazing properties
a_0=0.05;
theta_1=60*2*pi/360;
theta_2=asin(sin(theta_1)/1.52); % the angle of the refraction
a=a_0/cos(theta_2);
rho=0.5*((sin(theta_2-theta_1)/sin(theta_2+theta_1))^2)*(1+cos(theta_1+theta_2)^2/cos(theta_1-theta_2)^2)
trans=(1-rho)^2*(1-a)^2/(1-rho^2*(1-a)^2)
ODE Solver
function dT_dt=temp_Profile(t,T,t_S) % this is the ode for temperature distribution in the box-type solar cooker % Variables: % T : is a 5x1 array of temperatures in the following order: % T(1): Temperature of the lid of vessel, Tc % T(2): Temp of the sides and base of the vessel, Tsb % T(3): Temp of the cooking fluid, Tf % T(4): Temp of the lower glass cover, Tgl % T(5): Temp of upper glass cover, Tgu % t_S : Starting time in seconds, variable used to offset time from the ode % time to solar time % Initialization dT_dt=zeros(5,1); % Temperature load 'Lawrence_TMY3_June_21'; % Site data, TMY(1)=time(hrs); TMY(2)=Global horizontal Irradiation % TMY(3)=diffuse horizontal irradiation, TMY(4)=dry bulb temperature if ((t+t_S)/3600)<1 t_i=1; % [hrs] time of day else t_i=(t_S+t)/3600; end T_a=interp1(Lawrence_TMY3(:,1),Lawrence_TMY3(:,4),t_i); %[C] temperature of the ambient air % Absorber plate: gray body base, 'base' is the same as 'absorber' % Box material ???? k=0.03; %[W/mK] thermal conductivity of insulating material l_s=30*.0254; %[m] length of one of the sides of box w_s=30*0.0254; %[m] width of one of the sides of box h_s=12*0.0254; %[m] height of box x_b=1*0.0254; %[m] thickness of bottom insulating material x_s=3.25*0.0254; %[m] average thickness of insulating material on the sides n_opt=0.6; %[] efficience of inner reflector n_u=0.3; %[] overal utilization of cooker % Cooking Vessel: assum a cylindrical vessel % User entered data a_p=0.09; %[] absorptivity of cooking vessel E_c=1; %[] emissivity of the cooking vessel cover/lid r_v=3.75*0.0254; %[m] radius of the cooking vessel h_v=5*0.0254; %[m] height of the cooking vessel x_t=0.125*0.0254; %[m] thickness of the cooking vessel A_b=pi*r_v^2; %[m2] area of the base A_sb=2*pi*r_v*h_v+A_b; %[m2] area of the sides + base of cooking vessel A_s=2*pi*r_v*h_v; %[m2] area of the sides cooking vessel A_t=A_b; %[m2] area of lid of vessel h_ccl=convection_Air(T(1),T(4),(r_v/2),'Horizontal-Upper'); %(estimated=4)[W/m2K] convective heat transfer: wind %(estimated=3.777; todo list)[W/m2K] convective heat transfer: vessel to lower glass L_c_sbf=38*0.0254/(pi*3.75*2)+4.875*0.0254; % this is the height of vessel + charecteristic length of the base h_c_sbf=500; % h_c_sbf=convection_Water(T(2),T(3),L_c_sbf,'Vertical'); %(estimated=5)[W/m2K] convective heat transfer: walls to cooking fluid % ToDo - this convective heat coefficient does not take into account the % fact that some heat is transmitted through the base and some through the % side walls of the vessel. The characteristic length is calculated by % deviding the total surface area of the cooking vessel by the total % perimeter k_t=80; %(cast iron)[W/mK] thermal conductivity of cooking vessel material U_b=k/x_b; %[W/m2K] bottom loss coefficient % U_s=1/((x_s/k)+1/h_w); %[W/m2K] side loss coefficient U_t=5; %(estimated)[W/m2K] top loss coefficient m_c=0.531; %[kg] mass of the lid (added by JK) c_c=506; % [J/kgK] heat capacity of lid (added by JK) m_sb=5.675*0.454; %[kg] mass of sides and base of vessel(added by JK) c_sb=c_c; %[J/kgK] heat capacity of base+surfaces (added by JK) % Cooking fluid properties: Assume the food cooked is just water h_f=3*0.0254; %[m] height of cooking fluid in the cooking vessel rho_f=1000; %[kg/m^3] 1000 density of the cooking fluid c_f=4170; %[J/(kg.K)], 4170 specific heat capacity of cooking fluid m_f=(pi*(r_v-x_t)^2)*h_f*rho_f; % [kg] mass of cooking fluid A_sf=2*pi*(r_v-x_t)*h_f; %[m2] surface area of vessel covered by cooking fluid h_gap=3.17; %[W/m2K] convective heat transfer: fluid to ambient R_t=(1/h_gap)+(x_t/k_t)+(1/U_t); % thermal resistance: fluid surface and ambient % Cover/Aperture: assume double glaze % User entered variablesf x_g=0.1875*0.0254; %[m] 0.1875*0.0254 thickness of the cover a_g=0.05; %[] absorptivity of glass cover t_g=0.95; %(estimated)[] 0.95 transmissivity of glass density_g=2180; %[kg/m3] 2180 density of glass r=30*0.0254; %[m] width of the cover l_g=30*0.0254; %[m] length of the cover x_lu=0.5*0.0254; %[m] the air gap between upper and lower glass E_gl=1; % [] emissivity of lower glass E_gu=1; % [] emissivity of lower glass A_g=l_g*r; % [m2] area of glass h_clu=convection_Air(T(4),T(5),(r^2/(4*r)),'Horizontal-Upper'); %(estimated=3)[W/m2K] convective heat transfer: lower glass to upper glass h_w=convection_Air(T(5),T_a,(r^2/(4*r)),'Horizontal-Upper'); %(estimated=4)[W/m2K] convective heat transfer: wind h_rlu=4; %(estimated)[W/m2K] radiative heat transfer: lower glass to upper glass h_rua=4; %(estimated)[W/m2K] radiative heat transfer: upper glass to ambient k_g=1.38; %[W/mK] thermal conductivity of glazing material (added by JK) m_g=(x_g*r*l_g)*density_g; %[kg] mass of glass c_g=750; %[J/(kg.K)], specific heat capacity of glass % Reflector: the reflector outside the box % user entered values rho_o=.85; %[] 0.85 outer mirror reflectivity tilt=80*2*pi/360; %[degrees] 50 angle of outer reflector, convert to radians for % compatibility with MATLAB 2013+ c=30*0.0254; %[m] length of reflector w_r=c; %[m] width of reflector t_r=0.05;%[m] (estimated)thickness of reflector (added by JK) A_r=c*w_r; %[m] area of reflector s=sqrt(c^2+r^2-2*c*r*cos(tilt)); %[m] distance from the outer mirror to outer edge of cooker F_rg=(c+r-s)/2*r; %[] this is the view factor of the reflector-glass A_c=A_r+A_g; %[m2] aperture size is the total of A_reflector + A_window % Irradiance and environment: Assume that intensity is constant throughout the day h_angle=(t_i-12)*(2*pi/24); %[degrees] hour angle, starting at 12 noon Steph_Boltz=5.67*10^-8; %[W/m^2*K^4] Stephano-boltzmann constant I_h=interp1(Lawrence_TMY3(:,1),Lawrence_TMY3(:,2),t_i); %[W/m2] global irradiance on a horizontal surface, Lawrence, MA, June 21, TMY3 I_d=interp1(Lawrence_TMY3(:,1),Lawrence_TMY3(:,3),t_i); %(estimated)[W/m2] diffuse irradiance on a horizontal surface, Lawrence, MA, June 21, TMY3 I_b=I_h-I_d; % (estimated)[W/m2] beam irradiance on a horizontal surface, Lawrence, MA, June 21, TMY3 rho=0.2; %[] ground reflectivity rho_i=0.85; %[] inner mirror reflectivity lat=42.717*2*pi/360; %[degrees] latitude of site decl=23.45*2*pi/360; %[degrees] solar declination angle, June 21, Lawrence, MA R_b=(cos(lat-tilt)*cos(decl)*cos(h_angle)+sin(lat-h_angle)*sin(decl))/(cos(lat)*cos(decl)*cos(h_angle)+sin(lat)*sin(decl)); I_t=I_b*R_b+0.5*I_d*(1+cos(tilt))+0.5*rho*(I_b+I_d)*(1-cos(tilt)); %[W/m2] global irradiance on outer reflector I_ro=I_t*rho_o*F_rg*A_r/A_g; %[W/m2] irradiance reflected by outer reflector I_ri=(I_ro+I_h)*(t_g^2)*rho_i*n_opt; %[W/m2] irradiance reflected by inner reflector % Calculations of variables - these are the variables that depend on other % variables and temperature U_s=1/((x_s/k)+1/h_w); %[W/m2K] side loss coefficient % Calculating the view factor from cooking vessel cover to fluid % Assume circular disks, page 817 of Fundamentals of Heat.... L_cf=h_v-h_f; % [m] the distance between the cooking fluid and the cooking vessel cover r_c=r_v/L_cf;r_f=(r_v-x_t)/L_cf; % [] exactly from fundamentals of heat transfer book (check references) S=1+(1+r_f^2)/r_c^2; F_cf=0.5*(S-sqrt(S^2-4*(r_f/r_c)^2)); % [] view factor F % Calculating the view factor from cooking vessel cover to lower glass % Assume circular disks, page 817 of Fundamentals of Heat.... L_cl=7*0.0254; % [m] the distance between the top of the vessel to the lower glass r_c2=r_v/L_cl;r_l=r/L_cl; S=1+(1+r_l^2)/r_c2^2; F_cl=0.5*(S-sqrt(S^2-4*(r_l/r_c2)^2)); % [] view factor F % Calculating the view factor from the lower to upper glass % assume two rectangles parallel, page 817 of Fundamentals of Heat .. x_gl=r/x_lu;y_gu=r/x_lu; F_lu=(2/(pi*x_gl*y_gu))*(log(sqrt((1+x_gl^2)*(1+y_gu^2)))+... x_gl*sqrt(1+y_gu^2)*atan(x_gl/(sqrt(1+y_gu^2)))+... y_gu*sqrt(1+x_gl^2)*atan(y_gu/(sqrt(1+x_gl^2)))+.... -x_gl*atan(x_gl)-y_gu*atan(y_gu)); % Calculations of the defferential equations dT_dt(1)=((I_ro+I_h)*(t_g^2)*a_p*A_t-U_t*A_t*(T(1)-T_a)-Steph_Boltz*E_c*F_cf*A_t*(T(1)-T(3)))/(m_c*c_c); dT_dt(2)=(I_ri*a_p*(A_c-A_t)-h_c_sbf*A_sf*(T(2)-T(3))-(U_b*A_b+U_s*A_s)*(T(2)-T_a))/(m_sb*c_sb); dT_dt(3)=(Steph_Boltz*E_c*F_cf*A_t*(T(1)-T(3))+h_c_sbf*A_sf*(T(2)-T(3))-(A_t/R_t)*(T(3)-T_a))/(m_f*c_f); dT_dt(4)=((I_ro+I_h)*t_g*a_p*A_g+Steph_Boltz*E_c*F_cl*A_t*(T(1)^4-T(4)^4)+h_ccl*A_t*(T(1)-T(4))-Steph_Boltz*E_gl*F_lu*A_g*(T(4)^4-T(5)^4)-h_clu*A_g*(T(4)-T(5)))/(m_g*c_g); dT_dt(5)=((I_ro+I_h)*a_g*A_g+Steph_Boltz*E_gl*F_lu*A_g*(T(4)^4-T(5)^4)+h_clu*A_g*(T(4)-T(5))-Steph_Boltz*E_gu*A_g*(T(5)^4-T_a^4)-h_w*A_g*(T(5)-T_a))/(m_g*c_g);
